Dando sequência à série do Engenharia 360 sobre os grandes matemáticos da história, este artigo é dedicado ao francês, Pierre de Fermat (1601 - 1665), que contribuiu de forma significativa no campo da Matemática (e consequentemente nas ciências exatas).

Fermat foi simplesmente o precursor do cálculo! Esclarecendo melhor, antes de Newton e Leibniz iniciarem seu embate histórico sobre quem foi o pai do cálculo integral e diferencial, Fermat já estudava limites, derivadas e integrais, ainda sem o formalismo e rigor que viria alguns anos mais tarde.

Vamos conhecer um pouco mais sobre esse grande gênio da humanidade e suas contribuições? Então, leia o texto a seguir!

Sobre Pierre de Fermat

Quem era o ser humano por trás do gênio?

Pierre de Fermat foi, sem dúvidas, o grande nome da Matemática no Século XVII. Só não foi maior devido ao seu desinteresse em publicar suas descobertas, que só foram conhecidas em função da troca de correspondências com amigos, a quem comunicava seus feitos.

A saber, Fermat era advogado e membro da Suprema Corte Provincial de Tolouse (sudoeste francês). Matemática era seu passatempo e paixão particular. E, como dito antes, sua genialidade e criatividade nessa área foi conhecida por poucos do seu convívio.

As correspondências de Fermat e Mersenne

Pela análise de suas correspondências, ele parecia ser um homem envergonhado e reservado, afável e cortês. Embora fosse um gênio de primeira grandeza, se via como no máximo um sujeito inteligente e com algumas boas ideias. Sobre essas correspondências, houve grande troca entre outro matemático francês, o Padre Mersenne, que, na época, surpreendeu Fermat ao entrar em contato com ele; e Fermat o surpreendeu com a agilidade e método com que respondia às questões propostas por Mersenne.

Só como exemplo, Mersenne perguntou certa vez a Pierre se o número 100.895.598.169 era primo ou não (lembrem-se que na época não existiam calculadoras) - perguntas dessa natureza eram frequentes. E ele respondeu que esse número era o produto de 112.303 e 898.423, e que esses, sim, eram primos. Até hoje, ninguém sabe como ele descobriu isso!

E quais foram seus grandes feitos?

Em Teoria dos Números, seu gênio brilhou grandemente! Blaze Pascal, um jovem matemático do mesmo período e que também tinha sua cota de genialidade, ao comentar os trabalhos de Fermat sobre a Teoria dos Números, disse-lhe em uma carta: "procure alguém que possa segui-lo em suas pesquisas sobre números. Da minha parte, confesso que estão bem além de mim e sinto-me competente apenas para admirá-las". Contudo, nessa área, algumas provas se perderam e só foram provadas mais de um século depois, por Euler, outro cara de genialidade equivalente.

A criação da Geometria Analítica e do Cálculo

No ano de 1629, ele criou a Geometria Analítica como a conhecemos - que até hoje é uma pedra no sapato de muitos alunos no ciclo básico do ensino de Engenharia. E Descartes, em 1637, também fez contribuições e por vezes é atribuído a ele essa descoberta. Porém, todas as bases foram dadas por Fermat oito anos antes.

Já o Cálculo, que hoje sabemos ter sido formulado em paralelo por Newton e Leibniz, teve todas as suas bases preparadas por Fermat! Isso mesmo! Em uma carta descoberta apenas em 1934, Sir Isaac Newton afirma que suas primeiras ideias acerca do Cálculo vieram diretamente "da maneira pela qual Fermat traçava tangentes". Aliás, os trabalhos de Fermat nesta área datam de 1629, mais de uma década antes do nascimento de Newton e Leibniz.

Entendendo o Cálculo como a matemática de determinar retas tangentes a curvas e máximos/mínimos, então é importante reconhecer a contribuição e influência que Fermat teve sobre os gênios que viriam após ele.

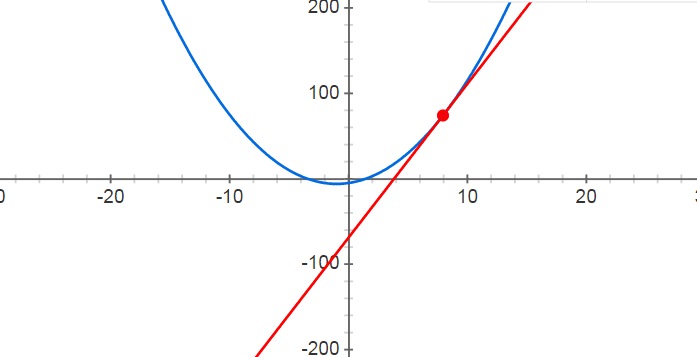
Há um caso em que Descartes, em tom desafiador, questiona os métodos generalistas de Fermat sobre a questão das tangentes e propõe que o método falharia para curva x³+y³=3axy (hoje conhecido como "folium de Descartes''). O próprio Descartes não conseguiu resolver esse problema e dizem que ficou mais louco ainda quando viu a bela e rápida solução apresentada pelo advogado por profissão e matemático por diversão, Fermat.

A palavra "gênio" deve sempre ser usada de forma adequada. Para Fermat, ela é absolutamente apropriada. Teve reconhecimento de matemáticos da época, fez avanços incríveis em Teoria dos Números e influenciou Newton e Leibniz. Gênio!

O último Teorema de Fermat

Como mencionado anteriormente, vários dos Teoremas de Fermat não tiveram suas provas, dada a banalidade com que ele mesmo tratava esses formalismos (se perguntavam a ele, ele respondia, senão, era seu passatempo). E, assim, muitos desses teoremas foram sendo provados mais de um século depois!

Mas restava um! O último!

A ideia é bem simples. Imagine a equação:

x²+y²=z²

Essa é uma equação bem conhecida e aparece no Teorema de Pitágoras. Pois bem, é sabido que existem soluções inteiras para x, y e z que satisfazem essa igualdade. Por exemplo:

3²+4²=5²

Ora, 3, 4 e 5 são soluções inteiras, assim como 5, 12 e 13. De fato, são várias terças dessa conhecidas desde os tempos de Euclides.

"É impossível separar um cubo em dois cubos, uma quarta potência em duas quartas potências ou, em geral, toda potência acima da segunda em duas potências de mesmo grau. Descobri uma prova verdadeiramente maravilhosa que essa margem é estreita demais para conter."

- nota feita por Fermat na aba de um livro.

Euler provou para o caso n=4 em 1747 e para n=3 em 1770; Gauss, Legendre e Dirichlet e outros resolveram par n=5 e 7. Além disso, é sabido que o Teorema é válido para n<125.000. Nessa linha, há especialistas que dizem que Fermat pode ter se enganado em uma prova geral para todo n. O fato é que todos outros teoremas propostos e que não foram apresentadas provas, foram provados ao longo dos anos. Enfim, será que ainda alguém duvida que Fermat tenha realizado mesmo essa prova?

Maldita seja aquela margem estreita do livro!

Imagens: Todos os Créditos reservados aos respectivos proprietários (sem direitos autorais pretendidos). Caso eventualmente você se considere titular de direitos sobre algumas das imagens em questão, por favor entre em contato com contato@engenharia360.com para que possa ser atribuído o respectivo crédito ou providenciada a sua remoção, conforme o caso.

Cristiano Oliveira da Silva

Engenheiro Civil; formado pela Escola Politécnica da Universidade de São Paulo; com conhecimentos em 'BIM Manager at OEC'; promove palestras com foco em Capacitação e Disseminação de BIM / Soft Skills.