O 360 já fez excelentes artigos sobre matemática aplicada. Mas, agora, nesta matéria, apresentamos como obter uma das mais belas identidades matemáticas utilizando as Séries de Maclaurin, a Identidade de Euler!

A saber, essa identidade contém as principais constantes matemáticas e foi descoberta por Leonhart Euler, um dos matemáticos mais brilhantes que a humanidade já conheceu. Continue lendo para saber mais!

Veja Também: Séries de Taylor e de Maclaurin

Um pré-entendimento das partes envolvidas na Identidade de Euler

O número imaginário 'i'

Qualquer estudante do Ensino Médio conhece o conceito do número 'i', que é um número imaginário definido como a raiz quadrada de -1. Esse domínio dos números complexos foi introduzido por René Descartes - já que não existe, no domínio dos números reais, a raiz quadrada ou qualquer raiz par de números negativos - de modo que, naquela época, acreditava-se que tais números não existiam.

Entretanto, ainda que "não existam", são ferramentas matemáticas muito úteis para relacionar grandezas correlatas - como, por exemplo, campos eletromagnéticos (campos elétricos e magnéticos). Na verdade, matematicamente falando, o domínio dos números complexos existe e suas aplicações são indiretas. Mas existe! Além disso, a sua utilidade se estende às soluções de equações algébricas e equações diferenciais.

As constantes 'π' e 'e'

Em outros momentos, apresentamos matérias explicando a origem do número "π" e do número "e". Há um universo de estudos dos matemáticos acerca desses números, amplamente utilizados por profissionais da área de exatas - e as suas particularidades podem até ser conferidas em algumas das matérias que já publicamos aqui no site!

A relação da função exponencial com as funções trigonométricas

Inicialmente, vamos observar as séries de Maclaurin para as funções e^x, sen(x) e cos(x):

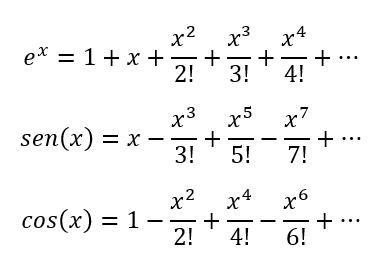
Se observarmos atentamente essas três expressões, é perceptível que elas se relacionam, a menos dos sinais dos termos. Ou seja: o sen(x) relaciona expoentes e fatoriais ímpares, ao passo que o cos(x) relaciona expoentes e fatoriais pares. Já a função e^x, relaciona expoentes e fatoriais pares e ímpares.

Mas será que há uma forma de relacionar a função exponencial com as funções trigonométricas? A resposta é sim, e o crédito dessa relação é atribuído a Euler!

Suponha que o expoente x seja substituído por “θi”, onde o θ seja um número real - um ângulo em radianos, por exemplo - e 'i' a constante imaginária.

Sabe-se que 'i' apresenta uma relação de recorrência quando elevado a um número natural, ou seja:

• i¹= i
• i² = -1
• i³ = -i
• i⁴ = 1
• i⁵ = i
• i⁶ = -1

E assim se repete...

Sabendo disso, vamos substituir “θi” na expressão da função exponencial:

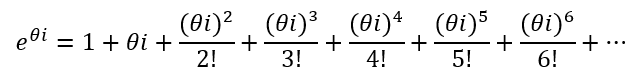
Substituindo os valores dos expoentes de 'i', a expressão pode ser reescrita da seguinte maneira:

Por fim, vamos colocar em ordem os termos em que aparecem 'i' e os que não aparecem:

Conseguem perceber o que acontece? Na primeira soma infinita, temos a função cos(θ) e na segunda expressão, fica i.sen(θ). Portanto, uma forma de escrever essa relação seria:

Essa expressão é bem conhecida dos Engenheiros Elétricos, que a utilizam para representar fatores de circuitos elétricos alternados!

Colocando no plano dos números complexos, fica evidente a sua utilidade:

Enfim, ela, a identidade

Mas, e se o ângulo θ for considerado como sendo π? Bem, aí basta substituirmos na expressão:

Logo,

Ou seja,

Esta é, portanto, uma relação que envolve as 5 principais constantes utilizadas na Matemática!

Na opinião do físico Richard Feynman, essa é a expressão mais bela de toda a Matemática. Já segundo Saloman Khan - Khan Academy -, “If this does not blow your mind, then you have no emotions”.

Particularmente, concordo com as afirmações! E você? Deixe a sua opinião nos comentários!

Fonte: Identidade de Euler.

Imagens: Todos os Créditos reservados aos respectivos proprietários (sem direitos autorais pretendidos). Caso eventualmente você se considere titular de direitos sobre algumas das imagens em questão, por favor entre em contato com contato@engenharia360.com para que possa ser atribuído o respectivo crédito ou providenciada a sua remoção, conforme o caso.

Cristiano Oliveira da Silva

Engenheiro Civil; formado pela Escola Politécnica da Universidade de São Paulo; com conhecimentos em 'BIM Manager at OEC'; promove palestras com foco em Capacitação e Disseminação de BIM / Soft Skills.