Os números "e" e pi já foram assunto por aqui, no Engenharia 360. Você deve lembrar que seus valores são, aproximada e respectivamente 2,7183 e 3,1415.

Surge daí esse problema interessante: quem é maior: “Dois vírgula muito elevado a três e pouquinho ou três e pouquinho elevado a dois vírgula muito?". Para se ter uma ideia de como os resultados são próximos, se você usar uma calculadora, chegará aos resultados 23,14 e outro 22,46.

Suponha que você não dispõe de calculadora, como saber quem é maior (a pergunta não é calcule os valores, mas quem é maior: um elevado ao outro ou outro elevado ao um).

Acompanhe a matéria!

Formulação do problema

Já tá formulado... quem é maior: e^pi ou pi^e?

Bem, para saber quem é maior, vamos definir uma relação entre esses números:

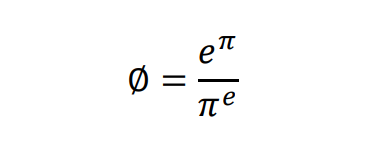
Função logarítmica

Então é possível aplicar a função logaritmo na base e, ou famoso ln (ou logaritmo natural ou logaritmo neperiano). Isso porque a função ln é injetora e crescente.

A título de curiosidade: a função logarítmica é inversa à função exponencial... então é um bom caminho utilizá-la.

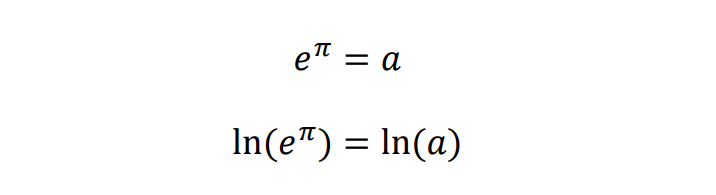
Da propriedade dos logaritmos, conclui-se que:

(o expoente “vem pra frente” e lne = 1)

Fazendo-se o mesmo para a outra parte:

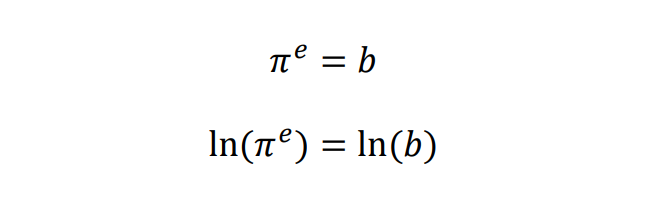
De onde se conclui que:

Certo... e o que fazer com isso?

Concordam se a > b ou a < b, então ln(a) > ln(b) ou ln(a) < ln(b)? (a desigualdade se mantém, ln x é função injetora e crescente!).

Então comparar

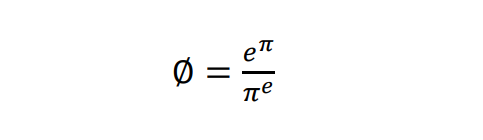
É o mesmo que comparar

Entendido isso, vamos para mais uma mudança de variável: seja ln⁡(π) = c (a título de curiosidade, se você calcular chegará ao número 1,145...).

Muito bem... Então, se...

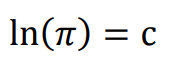
Novamente, das propriedades logarítmicas, nesse caso, usando a definição mesmo:

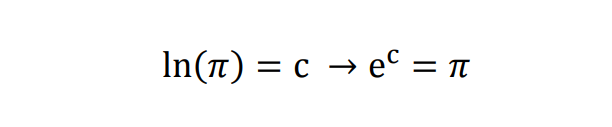
Observe essa expressão e a relação:

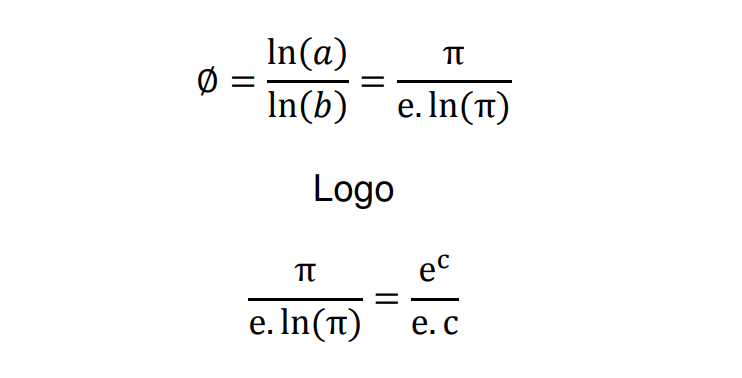
Pronto! Já podemos concluir quem é maior. Por que?

Percebam nessa última expressão, no numerador, que o número “e” aparece elevado a uma constante “c”; ao passo que no denominador o “e” aparece multiplicado por essa constante.

Sejam as funções f(x) = e^x e a função g(x)= e.x . 

Observe no gráfico abaixo seu comportamento, que dá respaldo para a afirmação do parágrafo anterior.

E o que isso significa? Que o numerador é maior que o denominador (na verdade, a única chance de ambos serem iguais é se c = 1. Qualquer outro número e^c será sempre maior que e.c).

..., como queríamos demonstrar!

Imagens: Todos os Créditos reservados aos respectivos proprietários (sem direitos autorais pretendidos). Caso eventualmente você se considere titular de direitos sobre algumas das imagens em questão, por favor entre em contato com contato@engenharia360.com para que possa ser atribuído o respectivo crédito ou providenciada a sua remoção, conforme o caso.

Cristiano Oliveira da Silva

Engenheiro Civil; formado pela Escola Politécnica da Universidade de São Paulo; com conhecimentos em 'BIM Manager at OEC'; promove palestras com foco em Capacitação e Disseminação de BIM / Soft Skills.