O número pi (π) é obtido através da razão do comprimento de uma circunferência por seu diâmetro. Essa definição é apresentada para qualquer aluno do Ensino Fundamental. Quem primeiro observou esse fato foram os Babilônios, há cerca de 2.000 a.C., quando propuseram que essa razão era aproximadamente 3.

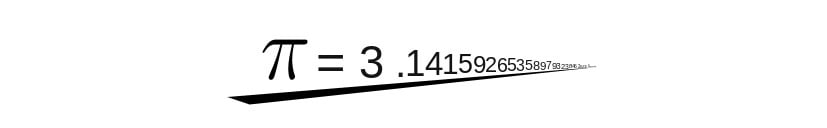
Veja Também: Equação desafia Inteligência Artificial avançada

A história do número pi (π)

Arquimedes de Siracusa (250 a.C.), famoso por cunhar a expressão “Eureka” após resolver um problema proposto pelo Rei Hierão, foi quem de fato estudou o número π mais a fundo sob o ponto de vista matemático. A ele atribui-se uma primeira aproximação, que é 22/7. Ele também concluiu que o número π está limitado entre 223/71 e 220/70. Uma forma mais elegante de apresentar esse intervalo é através da relação:

Ou seja, π está entre 3,140845 e 3,142857.

Em 1706 d.C. Willian Jhones, um matemático galês pouco conhecido que viria a se tornar vice-presidente da Royal Society de Londres no século XVIII, introduz o símbolo π para designar esse número.

Veja Também: A Matemática Responde - parte 1: quem é maior, e^pi ou pi^e?

A busca impossível pelo valor exato

Jamais saberemos o valor exato de π, uma vez que Johann Lambert prova em 1768 que o número é irracional (sei que estamos entre engenheiros e todos aqui sabem que um número irracional é um número que não pode ser expresso através de uma fração).

O valor das 20 primeiras casas de π é: 3,14159265358979323846...

Em 1862, o matemático alemão Ferdinand von Lindemann solucionou um dos problemas mais importantes associados a π, mostrando que ele era “transcendental”. O conceito de número transcendental é mais familiar aos matemáticos e menos a nós, engenheiros. Um número transcendental, basicamente, é aquele que não pode ser solução de uma equação algébrica (uma equação que envolva apenas potências de x).

Lindemann também solucionou um problema que durou gerações, que era a quadratura do círculo. Esse problema consiste em, dado um círculo, construir com quadrado de área igual utilizando apenas régua e compasso. Hoje em dia, graças a ele, sabemos que é impossível solucionar esse problema.

Diversos caminhos para π: Beleza matemática

Há muitas maneiras de se calcular o número π. E algumas são belíssimas!

Apresentaremos a seguir algumas maneiras.

O homem que viu o infinito

O gênio autodidata Srinivasa Ramanujan (cuja biografia é contada no filme “O homem que viu o infinito”), concebeu algumas fórmulas espetaculares para π. Uma delas é essa:

Ele acerta incríveis 6 casas decimais de π!

Só não me pergunte como o cara conseguiu chegar nessa expressão.

O cálculo computacional de π: Limites da tecnologia

Uma outra forma de se obter π é através da expansão do arco duplo.

É possível demonstrar que se

Então

Expandindo a expressão acima em arcos metades, chega-se à série infinita

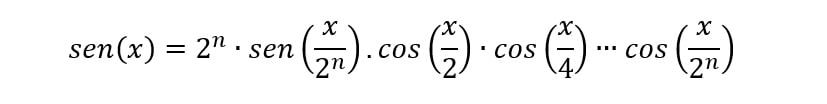
Para desenvolver essa expressão, é necessário resolver o limite:

É possível demonstrar que esse limite converge pra x, quando n tende a infinito, chegando-se à expressão:

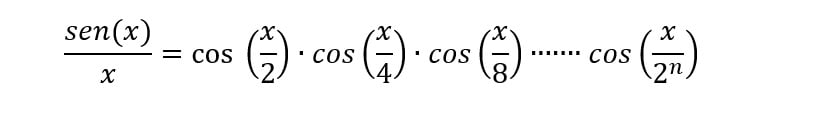
Sabendo-se que

Chegamos a uma expressão para o cos(x)

E assim sucessivamente...

Usando a mesma ideia de pegar arcos metade e considerando o valor de x = π/2, chegamos à belíssima expressão:

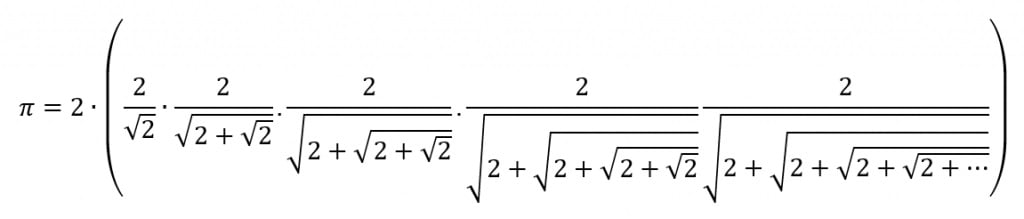
Cálculo via integral do arctan(x)

Com o advento do Cálculo Integral e Diferencial, outra expressão pode ser obtida para cálculo de π baseada no arctan(x).

Sabendo-se que a derivada do arctan(x) pode ser expressa por:

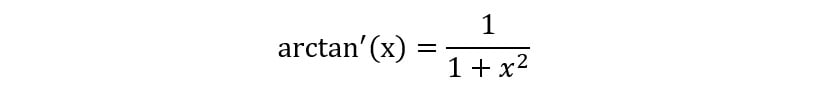
E que a soma dos infinitos termos de uma PG (progressão geométrica) de termo inicial igual a 1 e razão r = (-x²), converge para

Ou seja,

Obtemos então as seguintes igualdades matemáticas:

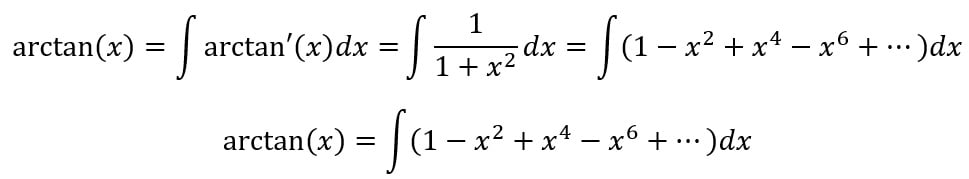
Qualquer aluno de 1º ano de Engenharia sabe resolver essa integral sem dificuldades e obterá a seguinte série infinita para o arctan(x):

Pergunta valendo a obtenção do π: qual é o arco, cuja tangente vale 1?

Se você lembrar do famigerado círculo trigonométrico, sabe de cara que esse arco é 45° ou... π/4

Substituindo o valor 1 na expressão do arctan(x) expresso na soma infinita acima, chegamos à expressão:

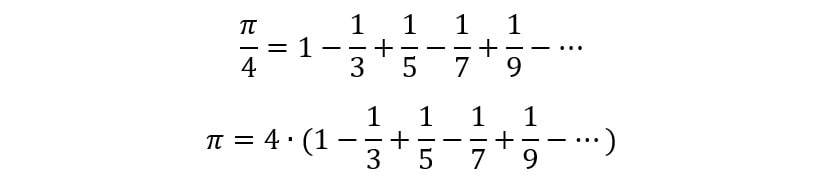
É uma das mais belas expressões matemáticas para π: embora seja um número irracional e transcendental, ele pode ser expresso como 4 vezes uma soma alternada infinita de frações com denominadores ímpares!

Curiosidades sobre essa série: sua convergência é extremamente lenta. Para ter uma ideia, a primeira casa decimal de π estabiliza-se apenas a partir do 30° termo. Para estabilizar a 2ª casa decimal, são necessários mais de 100 termos!

Usando a mesma ideia por trás da expansão em série de arctan(x), o mundo conheceu um matemático que não sabia “brincar”. Sir Isaac Newton encontrou uma série que, com apenas 10 termos, chega a estabilizar até a 6ª casa de π.

É possível demonstrar utilizando relações da tangente da soma de arcos, ou tan(a+b), velha conhecida ensinada no Ensino Médio que:

Fazendo as substituições devidas, chegamos a série de somas infinitas apresentada abaixo

Essa expressão pode não ser tão bela, mas converge que é uma beleza!

π: Mais do que um Número, uma Obsessão

Nos tempos modernos, foram sendo obtidas cada vez mais casas decimais desse número através do computador.

Em 1949, foram calculadas 2.037 casas decimais de π, o que levou longas 70 horas em um computador ENIAC. Em 2002, já tinham sido calculadas absurdas 1.241.100.000.000 (um trilhão, duzentos e quarenta e um bilhões e cem milhões!!!) casas decimais. E esse número não para de crescer. Para ter uma ordem de grandeza desse número: imagine que se estivéssemos na linha do equador e começássemos a escrever suas casas decimais, essa quantidade de números daria 62 voltas em torno do mundo!

Diversas questões têm sido perguntadas e respondidas acerca desse número. Serão os algarismos de π aleatórios? Há alguma sequência predeterminada na expansão? Até os anos de 1950, era impossível saber, já que eram conhecidas “apenas” umas 2000 casas. No ano de 1997, foram encontradas algumas sequências interessantes.

Utilizando-se o exercício mental da linha do equador, na posição 17.387.594.880, cerca de 1000km antes de completar uma volta na Terra, vocês encontrarão dez “6” seguidos. E deverá esperar até que uma volta seja completada e caminhar mais uns 5800 km até encontrar dez “7” seguidos.

Mas para que serve saber tantas casas decimais? Afinal, para os cálculos de engenharia, umas 2 casas decimais já resolvem nossos problemas. Esses cálculos extensos não são apenas por “diversão”: eles são usados para testar os limites dos computadores atuais, além de exercerem um fascínio sobre um grupo de matemáticos que se denominou “os amigos do pi”.

Desvendamos juntos os segredos de π. Compartilhe suas ideias e curiosidades sobre esse número incrível nos comentários!

Fontes:

• 50 maths ideas that you really need to know; Tony Crilly
• Elementos de Cálculo Diferencial e Integral; Granville; Longley

Imagens: Todos os Créditos reservados aos respectivos proprietários (sem direitos autorais pretendidos). Caso eventualmente você se considere titular de direitos sobre algumas das imagens em questão, por favor entre em contato com contato@engenharia360.com para que possa ser atribuído o respectivo crédito ou providenciada a sua remoção, conforme o caso.

Cristiano Oliveira da Silva

Engenheiro Civil; formado pela Escola Politécnica da Universidade de São Paulo; com conhecimentos em 'BIM Manager at OEC'; promove palestras com foco em Capacitação e Disseminação de BIM / Soft Skills.