Diferente do número “pi”, cuja investigação pelos Babilônios remonta a mais de 2000 a.C., o número ‘e’ é bem mais jovem no hall da fama matemático. A sua história começa de verdade no início do século XVII quando diversos matemáticos se empenharam na construção da ideia de logaritmo, uma daquelas grandes “sacadas” matemáticas que transformam a multiplicação de grandes números numa soma. Em 1618, John Napier encontra uma constante ‘e’ em conexão com esse conceito de logaritmos. O valor aproximado dessa constante matemática é 2,71828.
Então qual sua importância?
Essa constante aparece em tudo que envolve crescimento, seja em dinheiro, populações e outras quantidades físicas.
Jacob Bernoulli era um dos brilhantes “Bernoullis” da Suíça, uma família que supriu o mundo com uma dinastia de matemáticos. Em 1683, Jacob mergulhou fundo no problema dos juros compostos.
Dinheiro, dinheiro e mais dinheiro
Para nossos propósitos didáticos, vamos imaginar a seguinte situação: você dispõe de R$1,00 e deseja fazer uma aplicação. Como você é fera no mercado financeiro e sabe tudo de ações, consegue um investimento num fundo altamente agressivo que rende 100% no ano (sim, temos um exemplo hipotético e pouco provável na vida real... mas vamos seguir que você verá onde quero chegar...).
Se esse seu investimento rende 100% ao ano, no final de um ano significa que você terá dobrado seu capital, afinal a nossa super-taxa-hipotética é 100%. Então 100% de R$1.000,00 é R$1.000,00 e você então terá dobrado seu capital! Parabéns, você está numa galopada boa rumo à sua liberdade financeira. Vamos chamar de fator multiplicador a relação valor final / valor inicial. Arbitrariamente, vamos batizar esse número de ‘e’, no nosso caso, e = 2.
PUBLICIDADE
CONTINUE LENDO ABAIXO
LEIA MAIS
Mas, e se o período considerado, ao invés de 1 ano, fossem 6 meses e a taxa de juros fosse reduzida à metade? Então seriam 50% nos primeiros 6 meses e mais 50% nos 6 meses seguintes. Quanto você teria no final de 1 ano?
Ao final de 6 meses, a uma taxa de 50%, você teria um rendimento de R$500,00 e seu capital passaria a ser R$1.000,00 (iniciais) + R$500,00 (juros em 6 meses) e você teria então R$1.500,00. Dessa forma, nos próximos 6 meses, você teria mais 50% incidindo sobre esse montante de R$1500,00 (óbvio que estamos falando de juros compostos), que resulta em R$750,00. Perceba que o seu capital agora é R$1.500,00 + R$750,00 = R$2.250,00! O fator multiplicador ‘e’ agora é 2,25 (maior que o fm = 2 do período de 1 ano!). Será que descobrimos uma mina de ouro? Calma que isso tem um limite! Imagina que limite pode ser esse? Vamos simular mais um cenário:
O período agora é a cada 3 meses, ou ¼ de ano. Os juros, portanto, são reduzidos na mesma proporção, resultando em 25% a cada 3 meses.
Dessa forma, nos primeiros 3 meses, seu capital viraria R$1.250,00.
PUBLICIDADE
CONTINUE LENDO ABAIXO
Depois, em 6 meses, teria R$1.562,50.
Após 9 meses, R$1.953,13
E finalmente, após 1 ano, seu montante seria R$2.441,41.
Dessa maneira, ‘e’ é aproximadamente 2,44.
Acho que nesse ponto vocês já entenderam a lógica da situação: quanto menor o intervalo de tempo, maiores são os rendimentos para uma mesma taxa proporcional a esse período.
Se você fizer essa “brincadeira” e pegar períodos cada vez menores, por indução, podemos concluir que seu montante ao final do ano será sempre maior e o seu ‘e’ tende a crescer indefinidamente, certo? Errado! Se você fizer isso e considerar juros a cada segundo por exemplo, o ’e’ tende a um limite.
Na tabela a seguir, ilustramos esse valor do ‘e’ como função do intervalo de tempo:

Esse limite de crescimento contínuo num período infinitesimal, é o nosso famigerado número ‘e’!
O valor exato de "e"
Assim como seu primo mais famoso “pi”, “e” também é irracional e foi provado pelo grande gênio matemático Leonhard Euler em 1737. Demorou mais de 100 anos para que em 1873, o matemático Charles Hermite provasse que “e” era um número transcendental (número que não pode ser raiz de nenhuma equação algébrica). O método usado por Hermite para concluir esse fato, foi adaptado nove anos mais tarde para provar que “pi” também era transcendental, um problema considerado pelos matemáticos muito mais valioso.
O número ‘e’ é constantemente chamado “número de Euler”, também é chamado de “número natural” ou “número neperiano”.
Seu valor para as primeiras 20 casas decimais é 2,71828182845904523536....
Usando apenas frações, a melhor aproximação utilizando uma relação de números de 2 algarismos, 87/32, que resulta em 2,71875. Se colocar em uma fração de 3 algarismos, curiosamente 878/323, resulta em 2,71827, ou, arredondando, 2, 7183 (acerta 3 casas decimais)
Formas de obtenção
Cálculo da derivada da função exponencial e logarítmica
Mais uma vez, o Cálculo Integral e Diferencial mostra sua força e elegância. Vamos apresentar o conceito bem difundido de Derivada e vamos ver o que acontece ao considerarmos uma função exponencial. Será “natural” a obtenção do ‘e’.
Considere uma determinada função exponencial f(x) = ax.
A definição matemática de derivada, de forma simples e sem nos preocuparmos com os rigores matemáticos necessários para validar a existência dessa derivada, é a seguinte:

Sei que essa expressão já tirou o sono de muita gente aqui, mas ela é bem simples: dada uma função qualquer, você faz “delta y” sobre “delta x” e vê o que acontece quando esse “delta x” tende a zero!
Vamos substituir a nossa função f(x) = ax e dar uma trabalhada matemática nela para ver o que acontece?
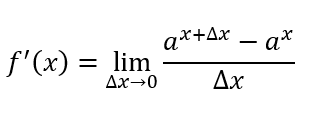
Utilizando a propriedade de potências, você pode colocar a nossa função f(x) em evidência, o que resulta:

A expressão acima pode ser escrita da seguinte forma:

O que isso significa?
Significa que, se você achar um número “a” qualquer, que faça o limite entre parênteses ser igual a 1, então a derivada da função é ela própria!
Então, vamos fazer isso e estimar que número “a” seria esse (a essa altura, você já deve estar desconfiado de que número iremos obter...).

Nosso objetivo agora, passa a ser achar um número “a”, tal que faça com que esse limite seja igual a 1.
Dessa forma:
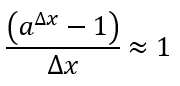
Então, isolando o número “a”, teremos a seguinte relação:
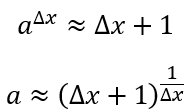
Para nossos propósitos, é conveniente pensarmos numa mudança de variável.
Vamos considerar um número n que tende a infinito quando Δx tende a zero.
Em “matematiquês”:

E fazendo isso, chegamos a:

Quando n tende a infinito, encontramos o número “e”:

Percebam que interessante essa expressão: a relação 1/n, quando n tende a infinito, é zero. Então dentro dos parênteses, a expressão tente a 1. Só que há um simples detalhe: o expoente da expressão é o mesmo n infinito! Ou seja: dentro do parênteses é um número muito próximo de 1, que, elevado ao infinito, resulta em um número finito!
Na tabela abaixo, apresentamos valores de ‘a’ para diversos valores de n:
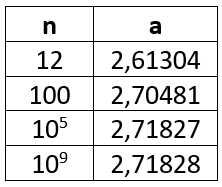
Então, o número ‘a’ que estamos procurando, é o número ‘e’!
(Isso faz o pessoal de humanas ficarem loucos! Como ‘a’ é igual a ‘e’? Que história é essa de letra ser igual a número...? E "a" ser igual a "e"?!?).
O fato é: quando a função exponencial tem como base o número "e", a sua derivada é igual à própria função.
Portanto, se f(x) = ex, então f’(x) = ex. Isso tem aplicações práticas diversas e é um grande facilitador ter uma função que ao derivá-la, resulta ela própria!
Se você fizer o mesmo processo para uma função logarítmica, você chegará ao mesmo número por um caminho diferente.
Fica uma ótima dica para o seu fim-de-semana: faça como exercício essa análise da derivada de uma função logarítmica qualquer e relembre os tempos em que você acreditava ser um Jedi da matemática!
Vou te ajudar: considere uma função logax
Se você calcular a derivada dessa função através da definição que utilizamos, você chegará à seguinte relação:
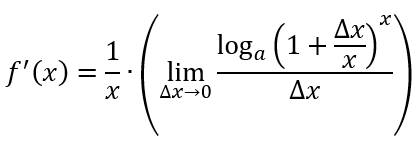
Ou seja, no caso da função logarítmica f(x) = logax, é possível provar que existe uma base “a”, tal que a sua derivada f’(x) resulta no inverso da variável x, ou seja 1/x.
Pois é, a base que iremos encontrar... é o número transcendental ‘e’.
Cálculo via série de potências
Através do polinômio de Taylor (que falaremos com mais detalhes em uma outra matéria), é possível calcular também o número ‘e’. Só pra matar sua curiosidade: o polinômio de Taylor é uma soma infinita das infinitas derivadas de uma função, com denominador expresso em números fatoriais consecutivos, conforme o grau da derivada e expoente de x de mesma ordem desse denominador.
(Se você é aquele/a engenheiro/a que “decorou” cálculo só pra passar, talvez tenha ficado um pouco confusa essa definição... mas vamos simplificar sua vida)
A definição do Polinômio de Taylor simplificada para nosso caso é a seguinte:
Dada uma função, diferenciável até infinito, define-se Polinômio de Taylor em torno de um ponto x0 = 0 a seguinte expressão:
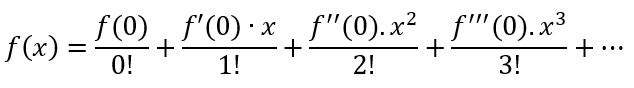
O que diz a série de Taylor é que qualquer função não polinomial, pode ser ajustada por um polinômio. O que é muito interessante.
Se f(x) =ex, então:

Já que f(x) = ex; f’(x) = ex; f’’(x) = ex; fn’ = ex... infinitamente!
Ou, ainda:

Então, se fizermos x = 1, teremos o valor de ‘e’ obtido da seguinte forma:
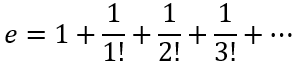
Os matemáticos (e por que não, nós engenheiros também?) são fascinados por simetrias e relações que apresentam alguma beleza intrínseca.
Perceba que o número "e", apesar de irracional e transcendental, pode ser expresso como uma soma infinita de frações muito bem definidas, como a que se apresenta.
Qual a importância do "e" então?
Como mencionado no início da matéria, tudo que envolve crescimento exponencial, envolve esse número.
Populações de bactérias que crescem de forma exponencial, dobrando sua quantidade num curto espaço de tempo; ramsters, coelhos, roedores em geral e a Shimmer (porquinha-da-Índia da Maitê, minha filha), crescem de forma exponencial.
Vimos no exemplo aplicado ao dinheiro, que o número ‘e’ é um limite de crescimento de um capital no tempo.
O número de Euler, (como eu prefiro chamar, em respeito ao Mestre), também é utilizado para modelagem de decaimento radioativo, teste do carbono 14 para estimar data de fósseis.
Mas não é só isso...
Ele também aparece em problemas sem ligação ao crescimento.
Pierre Montmort, no século XVIII, estudou um desafio de probabilidade, que era o seguinte: um grupo de pessoas vai almoçar e depois apanha seus chapéus. Qual a probabilidade de que ninguém pegue seu próprio chapéu? Pode-se demonstrar que essa probabilidade é 1/e (cerca de 37%). E mais: a probabilidade de pelo menos uma pessoa pegar seu próprio chapéu é o complementar desse número, ou seja, 1-1/e (cerca de 63%).
Outra aplicação, é no estudo de eventos raros. Trata-se da Distribuição de Poisson.
James Stirling alcançou uma aproximação notável ao valor fatorial n! envolvendo ‘e’ e ‘pi’;
Também é estudada em estatística, a famosa “curva de sino” da distribuição normal.
No que se refere à construção de OAE’s (Obras de Arte Especiais), a curva da catenária de uma ponte pênsil, pode ser ajustada numa curva exponencial como melhor arranjo para suspensão dos pendurais.
Além disso, temos a elegante relação das cinco principais constantes matemáticas.
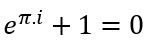
Salman Khan, que fundou em 2006 a Khan Academy(*) apresentando uma de suas aulas em um TEDTalks, ao ver essa expressão, disse:
“If this does not blow your mind, then you have no emotions!”
Salman Khan
(I have to agree...)
Fontes:
- 50 maths ideas that you really need to know; Tony Crilly
- Elementos de Cálculo Diferencial e Integral; Granville; Longley
E você, curtiu saber mais sobre esse primo caçula do número ‘pi’? Manda sua opinião aí que ela é sempre bem-vinda!
Comentários

Cristiano Oliveira da Silva
Engenheiro Civil; formado pela Escola Politécnica da Universidade de São Paulo; com conhecimentos em 'BIM Manager at OEC'; promove palestras com foco em Capacitação e Disseminação de BIM / Soft Skills.


