Segundo L. Kronecker, o nome de Gauss está ligado a quase tudo que a Matemática do século XIX criou em matéria de ideias científicas originais. Talvez tenha sido o matemático a melhor equilibrar a 'Matemática Pura' com a 'Matemática Aplicada'.

Bem, certamente você ouviu falar sobre Gauss no Ensino Médio, com plano de Argand-Gauss para o domínio dos números complexos, com a Lei de Gauss da Ótica e mais, não? E certamente depois, no Ensino Superior. Por exemplo, com o Teorema do Divergente - que relaciona integral de volume com integral de superfície; a Lei de Gauss para Eletromagnetismo; e Geometria Não-Euclidiana, contribuição no campo da Astronomia, desde desenvolvimento de lentes para telescópios até métodos para cálculo de órbitas; e muito mais!

Vamos conhecer um pouco mais sobre a história desse gênio da humanidade?

Apresentando o matemático Gauss

Carl Friedrich Gauss (1777-1855) foi o maior de todos os matemáticos e talvez o mais bem-dotado gênio de que já se teve notícia - em breve, neste texto, você entenderá o porquê.

Gauss nasceu em Brunswick, no norte da Alemanha. Sua familiaridade com números foi notada desde muito cedo, sendo que ele costumava brincar na vida que aprendera a contar antes mesmo de falar. Costuma-se dizer que Goethe escreveu e dirigiu peças para um teatro de bonecos quando tinha apenas 6 anos; que Mozart compôs seus primeiros minuetos quando tinha 5 anos; mas Gauss corrigiu um erro nas contas da folha de pagamentos de seu pai quando tinha 3 anos! Pode imaginar?

Infância

O pai de Gauss era um homem simples e não dispunha de recursos para ajudar a desenvolver os talentos do seu filho. Entretanto, as habilidades de Gauss com os números e cálculos mentais eram evidentes e chamou a atenção de muitos homens influentes de sua comunidade, entre eles, o duque de Brunswick, que acabou por financiar a sua educação.
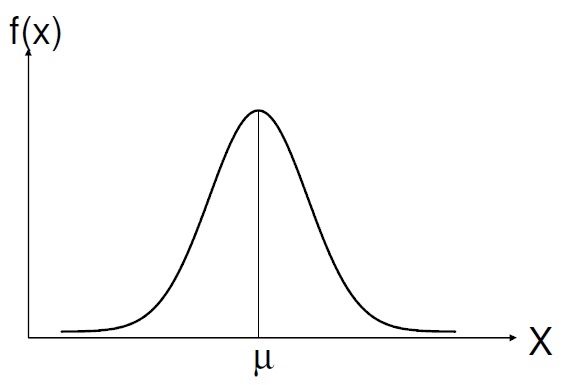
Dessa maneira, por volta dos 15 anos, já conhecera os trabalhos de Newton, Euler e Lagrange. Foi quando descobriu o Teorema do Número Primo. Nesse mesmo período, ele inventou o Método dos Mínimos Quadrados e concebeu os conceitos da famosa “Curva Normal” ou "Curva Gaussiana", relacionada à Distribuição na Teoria das Probabilidades. Isso aos 15 anos!

Adolescência

Na faculdade, não se sentia atraído pelos cursos de Matemática - vai saber, talvez fossem enfadonhos para ele, como seria para um aluno de Engenharia ter aulas sobre adição e subtração. Durante um tempo, seu futuro foi incerto. Mas aos 18 anos, fez uma bela descoberta em Geometria e acabou se decidindo por Matemática. E que descoberta foi essa? Os gregos antigos sabiam construir, com régua e compasso, polígonos regulares de 3, 4, 5 e 15 lados - e todos aqueles que podem ser obtidos dividindo os ângulos em 2 partes iguais. Isso era tudo que sabiam e esse problema ficou desse jeito, em aberto, por 2.000 anos, até que o jovem de 18 anos resolveu o problema completamente, provando que outros polígonos podem ser construídos se respeitada determinada condição.

Suas contribuições iniciais nesse período foram ao campo da Teoria dos Números, onde mergulhou profundamente em vários campos inexplorados. Seu tratado Disquisitiones Arithmeticae, publicado em 1801 - mas finalizado em 1798 - é considerado um marco do início da moderna Teoria dos Números, cuja importância para a Matemática é comparada aos Principia de Newton. Esse trabalho como um todo era um farto banquete de pura Matemática que seus sucessores só puderam digerir com dificuldade e lentamente.

Nesse trabalho, Gauss também criou a abordagem rigorosa e moderna da Matemática. Isso porque ele havia se tornado bastante impaciente com a escrita descuidada e desleixo de seus predecessores. Decidiu então que suas obras estariam acima de qualquer crítica, como escreveu: “Eu entendo a palavra 'prova', não no sentido do advogado, para quem 2 meias provas equivalem a uma prova completa, mas no sentido do matemático, para quem ½ prova = 0 e se exige uma demonstração que qualquer dúvida torne-se impossível.”.

Juventude

Disquisitiones revela um Gauss austero, maduro, rigoroso, sem comentários e, em alguns pontos, quase ininteligível. Segundo ele próprio em uma carta, “(...) sou lento para escrever. Isso ocorre principalmente porque não me satisfaço enquanto não consigo colocar o máximo de informação no menor número de palavras possível, e escrever de forma concisa leva muito mais tempo do que ser prolixo.”. Por conta disso, suas publicações ocultavam tanto quanto revelavam, uma vez que ele próprio conscientemente trabalhava para remover qualquer traço de linha de raciocínio que o havia levado às suas descobertas. Um amigo comentou: “Ele é como uma raposa que apaga a sua pegada na areia com o rabo.”. Gauss rebatia as críticas dizendo que nenhum arquiteto que tenha respeito próprio deixa os andaimes depois de terminada a construção.

A dissertação de doutoramento foi em 1799, outro marco na história da Matemática. Após várias tentativas frustradas de matemáticos anteriores - como D’Alembert, Euler, Lagrange e Laplace -, o Teorema Fundamental da Álgebra foi provado. Esse teorema afirma que todo polinômio com coeficientes reais ou complexos - tem uma raiz real ou complexa. Nessa primeira demonstração, ele apresentou quatro ao todo; e Gauss foi o primeiro matemático a usar números complexos e a Geometria no Plano Complexo com total segurança.

Fase adulta

Nesse próximo período da sua vida, Gauss se dedicou à Matemática Aplicada e seus “passatempos” com Teoria dos Números ficariam em suspenso por um tempo.

Nas últimas décadas do século XVIII, muitos astrônomos procuravam um planeta entre Marte e Júpiter. O primeiro e maior dos numerosos planetas menores - hoje, conhecido como asteroides - foi descoberto naquela região em 1801 e foi chamado de Ceres. O ponto é que esse “planeta” era muito pequeno e se perdeu no céu, ou seja, era muito difícil de ser visto nas melhores condições, logo perdido na luz do céu próximo ao Sol.

O "pequeno planeta" Ceres

Os esparsos dados obtidos da observação dificultaram o cálculo da órbita com precisão suficiente para localizar Ceres. Foram vários meses de tentativas frustradas. Finalmente, Gauss foi atraído pelo desafio. Pegou os dados de que dispunham os astrônomos, aplicou o seu Método dos Mínimos Quadrados aliado à sua destreza com os cálculos numéricos e determinou a órbita, contando aos astrônomos para onde deveriam mirar seus telescópios; e lá estava o “planetinha”.

Isso lhe rendeu fama, um aumento da pensão recebida do duque e, em 1807, uma nomeação como professor de Astronomia e primeiro diretor do novo observatório em Göttingen. Se encarregou de suas atribuições com a costumeira eficácia, mas mostrou-se avesso ao trabalho administrativo, reuniões, burocracias, etc. Também não se sentia motivado a ensinar. Dizia que era uma perda de seu tempo e essencialmente inútil, por razões diferentes, tanto para os alunos talentosos, quanto para os “meia-boca”. Recebeu diversos convites para deixar Göttingen, mas recusou todas as ofertas e lá permaneceu até o final de sua vida.

A coletânea de trabalhos de Gauss

Nas primeiras duas décadas do século XIX, Gauss produziu uma série de trabalhos sobre Astronomia, entre eles, o tratado Theoria Motus Corporum Coelestium, de 1809; essa foi a “bíblia” dos astrônomos por mais de um século. Seus métodos para lidar com perturbações levaram à descoberta de Netuno. Gauss pensava na Astronomia como sua profissão e na Matemática Pura como recreação e, de tempos em tempos, publicava alguns frutos de suas pesquisas individuais. A saber, datam dessa época seus estudos sobre Séries Hipergeométricas, que foi uma proeza tipicamente gaussiana, que envolveu novas ideias em análise e que mantém os matemáticos ocupados e com lição de casa desde então.

Por volta de 1820, o matemático foi chamado pelo governo de Hanover para supervisionar um levantamento topográfico no reino. Um trabalho tipicamente enfadonho, inclusive nos dias de hoje - exceto quando usamos drones, que, obviamente não existiam na época de Gauss, mas posso apostar que o Drone tem alguma contribuição de Gauss em sua tecnologia. Para ele, seria natural recusar esse trabalho exaustivo e com tediosas triangularizações. Mas, afinal, seria um desperdício usar uma mente tão avançada num trabalho desses? Certo? Errado!

O levantamento topográfico de Hanover

Mentes brilhantes têm a estranha característica de buscar enxergar as coisas por todas as óticas possíveis. Então, durante esse trabalho “tedioso”, Gauss forneceu profundas contribuições para a Matemática Pura, sem as quais a Teoria Geral da Relatividade teria sido totalmente impossível de ser formulada. O trabalho de Gauss sobre geodésicas e medição precisa de grandes triângulos na superfície terrestre. Isso gerou mais um trabalho em 1827, o “Disquisitiones generales circa superficies curvas”. Nesse trabalho, ele lança a Geometria Diferencial Intrínseca das Superfícies e introduz coordenadas curvilíneas numa superfície, já que a superfície terrestre é curva.

O nome dessa Geometria é bonito, mas a ideia por trás é simplesmente brilhante! Gauss descobriu um método para estudar a superfície estando sobre a mesma, apenas medindo distâncias e determinando o caminho mais curto de um ponto a outro - a tal geodésica. E, além disso, ele descobriu um método de medir a curvatura da Terra e qualquer outra superfície curva sem precisar se preocupar com o espaço à volta.

Outras coisas grandiosas que Gauss fez nesse período:

• apresentou, em 1831, artigo sobre resíduos biquadráticos;
• ampliou a Teoria dos Números para o domínio dos complexos - por exemplo, com a definição de inteiros complexos, hoje chamados inteiros gaussianos;
• introduziu um novo conceito de número primo, no qual 3 permanece primo, mas 5 = (1+2i).(1-2i) não;
• e provou o teorema da fatorização única para esses inteiros e primos.

Os estudos na área da Física

Gauss também, nesse período, direciona a sua atenção para a Física, dando contribuições originais e significativas sobre todo assunto que se debruçou. Para começar, na Teoria de Tensão de Superfícies, desenvolveu a ideia fundamental de conservação de energia e resolveu o mais antigo problema do cálculo variacional, envolvendo uma integral dupla com extremos variáveis. Já em Óptica, além da formulação matemática, introduzindo conceito de distância focal de um sistema de lentes e inventou as lentes grandes angulares de Gauss para telescópios e objetivas. Criou a ciência do geomagnetismo…

Inclusive, Maxwell publicou seu trabalho sobre Eletromagnetismo em 1873 e há diversas referências a Gauss nele. No prefácio, o matemático disse: “Gauss dirigiu seu poderoso intelecto para a teoria do magnetismo e para os métodos de observação, e ele não só contribuiu grandemente para aumentar nosso conhecimento na Teoria da Atração, mas reconstruiu toda a Ciência do Magnetismo no que diz respeito aos instrumentos usados, métodos de observação e cálculo dos resultados…”.

Em 1839, Gauss publicou seu artigo fundamental sobre a Teoria Geral das Forças Proporcionais ao Inverso do Quadrado, que estabeleceu a Teoria do Potencial como um ramo coerente da Matemática. Entre as descobertas, estavam o Teorema do Divergente da análise vetorial moderna, também chamado de Teorema de Gauss; além do Teorema do Valor Médio, para funções harmônicas.

A genialidade do matemático

Conhecemos algumas contribuições de Newton, bem como a genialidade de Fermat, o brilhantismo de Euler… Mas Gauss parecia sobre-humano!

Falamos de suas publicações, contribuições à Ciência, vida profissional de astrônomo, passatempo matemático; tudo isso já faria dele alguém com muita relevância na nossa espécie.

A questão é que o que ele não publicou, as suas pesquisas pessoais - o tornariam igualmente grande!

Muito desse material só apareceu após sua morte, quando uma grande quantidade de anotações de seus cadernos e correspondências científicas foram cuidadosamente analisadas e incluídas em seus trabalhos. Nesse material, encontra-se uma relíquia da história da Matemática: um caderno de 19 páginas, que permaneceu desconhecido até 1898. As anotações datam de 1796 até 1814 e consistem em 146 enunciados concisos, avesso à prolixidade ou ao estilo do próprio Gauss. Para se ter uma ideia, se ele não tivesse feito NADA do que foi publicado, apenas o conteúdo deste caderno já o tornaria o maior matemático de seu tempo!

Era muito comum que pessoas do círculo de Gauss e da comunidade científica trouxessem a ele um problema como “novo” e encarar a frustração de que Gauss já havia se debruçado sobre aquele problema e extraído tudo quanto fosse possível.

“Não é o conhecimento, mas o ato de aprender; não é a posse, mas o ato de chegar lá, que garantem maior satisfação. Quando esclareci e exauri um assunto, o deixo de lado para mergulhar novamente na escuridão.” - Gauss, em correspondência para Wolfgang Bolyai.

A urgência por um novo problema

Nota-se claramente que Gauss não queria perder tempo sobre o que descobria, mas tinha urgência em mergulhar num novo problema e tirar o máximo dele.

Um exemplo claro disso remete à Geometria Não-Euclidiana. Havia um postulado desde o tempo de Euclides. Muitos matemáticos tentaram prová-lo, sem sentido. Gauss, aos 15 anos, também falhou, mas como ele não dava “viagem perdida”, chegou a conclusão de que a geometria euclidiana não era a única possível. Em se tratando de Gauss, se havia outras geometrias possíveis, então o próximo passo era formular com critério. E como ele não quis publicar seus resultados, os créditos pelos Teoremas da Geometria Não-Euclidiana foram para Lobachevsky (1829) e Johann Bolyai (1832 - filho de Wolfgang).

Longe dos holofotes

Mas o que explica Gauss não publicar? Bem, uma carta enviada a Bessel, em 1829, pode dar uma pista. Nela, está dito o seguinte: “Não irei dedicar muito dos meus esforços para escrever algo publicável sobre esse assunto, pois tenho horror aos gritos histéricos que ouviríamos dos beócios se eu tornasse claros meus pensamentos sobre o assunto.”.
Lembrando que, nessa época, a filosofia estava em alta e alguns filósofos, como Kant, por exemplo, viam a Geometria Euclidiana como única forma possível de pensar o espaço.

Outro matemático muito famoso contemporâneo de Gauss, Jacobi, ao ver uma passagem em Disquisitiones, percebe que era preciso saber sobre funções elípticas para o conteúdo que encontrou. Então, em seguida, foi até Gauss e descobriu que ele havia avançado muito em assuntos que o Jacobi trouxe, mas que Gauss já tinha domínio antes mesmo do jovem matemático ter nascido.

Em carta ao seu irmão, Jacobi afirma: “a Matemática estaria numa posição muito diferente se a Astronomia prática não houvesse desviado esse gênio colossal de sua grandiosa carreira”.

Assim era Gauss, o supremo matemático. Ele sobrepujou em tantos aspectos as realizações possíveis para homens comuns com gênio que por vezes pode-se ter a misteriosa sensação de que ele pertencia a uma espécie superior.

Em um trecho do filme “Don’t look up”, a personagem interpretada por Leonardo diCaprio, em uma tentativa de garantir que a órbita do recém descoberto cometa estava certa, diz que “a órbita foi calculada pelo método de Gauss, com erro de 0,02%”. Mas quem foi Gauss? Agora você já sabe!

Veja Também: Série Grandes Matemáticos - Pitágoras, Euclides e Arquimedes

Fontes: Cálculo com Geometria Analítica – Vol I

Imagens: Todos os Créditos reservados aos respectivos proprietários (sem direitos autorais pretendidos). Caso eventualmente você se considere titular de direitos sobre algumas das imagens em questão, por favor entre em contato com contato@engenharia360.com para que possa ser atribuído o respectivo crédito ou providenciada a sua remoção, conforme o caso.

Cristiano Oliveira da Silva

Engenheiro Civil; formado pela Escola Politécnica da Universidade de São Paulo; com conhecimentos em 'BIM Manager at OEC'; promove palestras com foco em Capacitação e Disseminação de BIM / Soft Skills.