Se você está mergulhando nos primeiros semestres do curso de engenharia, já deve ter se deparado com nomes complicados, fórmulas gigantes e aquela sensação de “será que vou usar isso algum dia?”. Pois bem: a Equação de Bernoulli é um desses conceitos que parecem distantes, mas que, na prática, estão literalmente em todo lugar. Do funcionamento do chuveiro na sua casa ao voo de aviões comerciais, esse princípio é um dos pilares da mecânica dos fluidos e, consequentemente, da engenharia como um todo.

Neste artigo, você vai entender de forma simples (mas sem perder o rigor técnico) como a equação surgiu, quais são suas aplicações, como deduzí-la e por que ela pode ser sua aliada em diferentes áreas da engenharia.

Quem foi Daniel Bernoulli e por que ele é tão importante na História da Engenharia?

A equação leva o nome de Daniel Bernoulli, matemático neerlandês-suíço que publicou em 1738 o livro Hydrodynamica, onde apresentou sua famosa teoria. Ele foi um dos pioneiros em aplicar a ideia de conservação de energia ao estudo dos fluidos.

Para Bernoulli, um fluido em movimento obedece a um princípio fundamental: quando a velocidade de um fluido aumenta, sua pressão diminui — e vice-versa. Essa simples relação, que parece intuitiva, foi revolucionária e ajudou a explicar fenômenos que vão desde a circulação sanguínea até o voo dos aviões.

O princípio de Bernoulli em uma frase

De forma resumida: “A soma da pressão, da energia cinética e da energia potencial de um fluido é constante ao longo de uma linha de corrente, se o escoamento for ideal (sem viscosidade e incompressível).”

Isso significa que se o fluido ganha velocidade, ele “perde” em pressão ou altura, mantendo o balanço de energia. É como um jogo de troca: nada se perde, apenas se transforma.

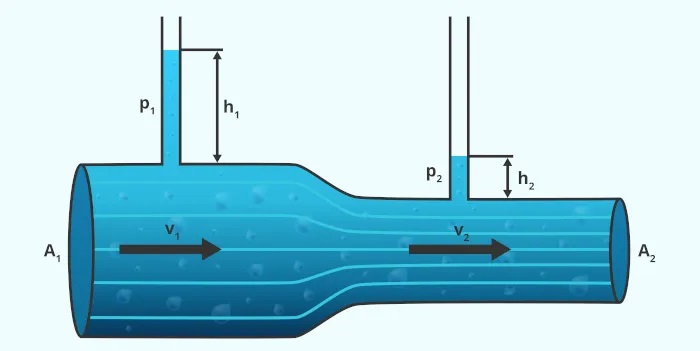
A forma clássica da equação

Para um fluido incompressível e sem viscosidade, sob ação da gravidade, a equação pode ser escrita como:

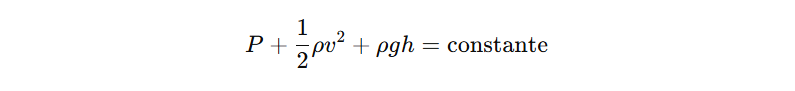
Onde:

• P = pressão
• ρ (rho) = densidade do fluido
• v = velocidade do fluido
• g = aceleração da gravidade
• h = altura em relação a um referencial

Essa é a forma que você provavelmente verá nos livros e nas provas. Cada termo representa uma forma de energia: pressão (energia de pressão), velocidade (energia cinética) e altura (energia potencial gravitacional).

As condições para usar a Equação de Bernoulli

Antes de sair aplicando essa fórmula em qualquer situação, é importante lembrar que ela só funciona em cenários específicos. Para valer, é preciso que:

1. O escoamento seja incompressível (densidade constante).
2. O fluido seja não viscoso (sem atrito interno).
3. O escoamento esteja em estado estacionário (não muda com o tempo).
4. A análise seja feita ao longo de uma linha de corrente.

Ou seja, estamos falando de uma simplificação da realidade. No entanto, essa simplificação é extremamente útil e funciona muito bem em diversos problemas práticos.

Exemplos práticos da Equação de Bernoulli no seu dia a dia

Agora vem a parte que interessa a todo estudante de engenharia: aplicações reais. Veja como a Equação de Bernoulli explica fenômenos que você já viu, mas talvez não tivesse percebido a física por trás.

1. Aviões voando

As asas dos aviões são projetadas para que o ar que passa por cima se mova mais rápido do que o que passa por baixo. Resultado: a pressão em cima da asa é menor que embaixo, gerando a força de sustentação. Sem Bernoulli, não haveria voo.

2. Chuveiro ligado

Quando você liga o chuveiro, a água passa por tubulações estreitas. Segundo Bernoulli, ao aumentar a velocidade, a pressão local diminui — é isso que ajuda a criar aquele efeito de spray.

3. Atomizadores e sprays

Perfumes, inseticidas e até carburares antigos de carros funcionam porque o ar em alta velocidade diminui a pressão em uma região, sugando o líquido e transformando-o em névoa.

4. Tubulações industriais

Em projetos de engenharia civil, mecânica e química, Bernoulli é aplicado para calcular a perda de carga, a pressão em bombas e o dimensionamento de tubulações.

5. Esportes

Desde o chute curvado no futebol (efeito Magnus) até a trajetória de uma bola de beisebol, os princípios de Bernoulli ajudam a explicar como o ar interage com objetos em movimento.

Fluídos compressíveis

Quando o fluido pode ser comprimido (como gases em altas velocidades), a equação ganha novos termos. Nesse caso, entra em cena a entalpia e a análise fica mais complexa.

A equação mais geral passa a considerar energia interna e processos adiabáticos. É nessa versão que os engenheiros aeronáuticos e mecânicos se debruçam para projetar turbinas, foguetes e motores a jato.

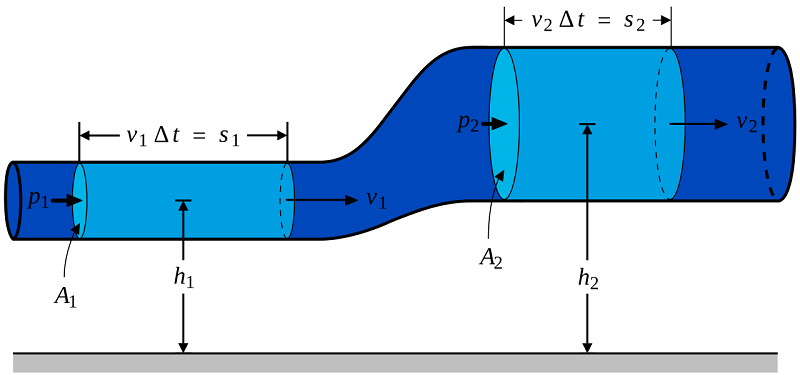
Dedução da equação: um resumo rápido

A Equação de Bernoulli pode ser deduzida a partir da conservação de energia. Imagine um fluido em movimento:

• O trabalho realizado pelas forças no fluido +
• A redução na energia potencial +
• O aumento na energia cinética

Dá como resultado a famosa equação.

Ou seja, Bernoulli nada mais fez do que aplicar a lógica da conservação de energia em um sistema de fluidos.

Relação com pressão hidrostática e altura de carga

Na prática, os engenheiros gostam de falar em “carga” ao usar Bernoulli:

• Carga de pressão (P/ρg)
• Carga de velocidade (v²/2g)
• Carga de altura (h)

Somando todas, temos a carga total de energia do fluido. Essa forma é muito usada em hidráulica, porque facilita visualizar como bombas e turbinas interagem com a energia do sistema.

E quando Bernoulli falha?

Nem tudo são flores. Existem situações em que a Equação de Bernoulli não pode ser aplicada de forma direta:

• Escoamentos com alta viscosidade (como óleo pesado).
• Fluidos turbulentos, em que a velocidade varia caoticamente.
• Sistemas com trocas de calor intensas, que quebram a premissa de conservação de energia mecânica.
• Situações com choques, onde variáveis mudam abruptamente (embora a constante de Bernoulli ainda possa ser útil em alguns casos).

Por que isso é essencial para sua carreira em engenharia?

Para você, estudante de engenharia, entender a Equação de Bernoulli é um passo fundamental para compreender a base de várias disciplinas e se destacar como profissional.

Dominar Bernoulli é como ter uma chave que abre várias portas. Ele conecta teoria e prática, matemática e realidade.

Você pode estar pensando: “Ok, entendi a equação, mas onde isso vai me ajudar no futuro?”. A resposta é: em praticamente qualquer área.

• Engenharia Civil: dimensionamento de adutoras, sistemas de bombeamento e projetos hidráulicos.
• Engenharia Mecânica: turbinas, motores a combustão e sistemas pneumáticos.
• Engenharia Química: transporte de fluidos em reatores e processos industriais.
• Engenharia Aeronáutica: aerodinâmica de asas, hélices e turbinas.
• Engenharia Ambiental: análise de fluxos de rios e esgoto.

Veja Também: 9 Equações que mudaram o mundo da Engenharia

---

Fontes: Wikipédia, UOL.

Imagens: Todos os Créditos reservados aos respectivos proprietários (sem direitos autorais pretendidos). Caso eventualmente você se considere titular de direitos sobre algumas das imagens em questão, por favor entre em contato com contato@engenharia360.com para que possa ser atribuído o respectivo crédito ou providenciada a sua remoção, conforme o caso.