Na Matemática, o estudo das séries de potências aplicadas a casos particulares é bem amplo e há diversos tipos a serem estudados, a exemplo das séries infinitas, de Fourier, de Taylor, de Maclaurin, binômio de Newton e por aí vai. Agora, neste texto do Engenharia 360, exploramos os dois tipos mais conhecidos: as Séries de Taylor e de Maclaurin!

Antes de tudo, vale dizer que a lógica por trás de uma aproximação por séries de potências é a seguinte: qualquer função que respeita algumas regras matemáticas de continuidade e diferenciação num intervalo dado, podem ser aproximadas por uma série infinita de polinômios.

Isso tem ganhos muito práticos, principalmente porque muitas vezes é mais fácil trabalhar algebricamente com polinômios do que com a própria função. Continue lendo para saber mais!

O que são Séries de Potências na Matemática?

Uma série de potências é toda expressão no formato:

Vejam que é uma soma infinita, do ponto de vista formal. Entretanto, na prática, é possível estimar um número finito de termos, tendo como premissa a precisão que se busca para a aproximação. Ou seja: pode-se avaliar o “erro”, pegando-se o último termo da série e subtraindo-se o valor do penúltimo. Não daremos foco nos formalismos matemáticos, mas na aplicação para o caso de algumas funções.

Veja também: Não sou bom em matemática, posso fazer engenharia?

Séries de Taylor

Na Matemática, a Série de Taylor é uma expressão que aproxima uma dada função em torno de um ponto escolhido arbitrariamente.

A expressão é a seguinte:

A constante c indica que a aproximação é válida em torno desse ponto. E os valores dos coeficientes a_n são definidos através das derivadas da função que se quer aproximar.

Utilizando-se essa ideia, chega-se à seguinte expressão:

Os termos f’; f’’, f’’’... correspondem às sucessivas derivadas da função que se quer aproximar.

Por exemplo: suponha que se deseje, através dessa série, calcular o valor aproximado para ln(2,1) (logaritmo neperiano de 2,1). Há tabelas de logaritmos para ln2, ln3, ln4, etc. Mas não é comum encontrar na tabela o valor do ln2,1. Se você pegar a sua HP empoeirada na gaveta e calcular esse valor, irá chegar a 0,7419373. E se você não dispusesse de uma calculadora para realizar esse cálculo? Uma saída seria usar o polinômio de Taylor!

A função em questão é ln(x). Vamos aplicar esse polinômio com os 4 primeiros termos e ver o que acontece?

Suas derivadas são bem conhecidas:

f’(x) = 1/x

f”(x)= -1/x²

f’’’(x) = 2/x³

Como queremos avaliar através da matemática a função para 2,1 então é bem razoável tomarmos a = 2. É em torno desse número que a expressão será calculada.

Substituindo então a = 2 no valor das expressões para as derivadas, temos:

f'(c) = 1/2

f’’(c) = -1/4

f’’’(c) = 1/4

Então, dessa forma, chega-se à expressão:

Substituindo-se x = 2,1 na expressão e os valores das derivadas, temos:

Resolvendo essa expressão, chega-se a 0,7419885, que é um valor que bate com o da calculadora até a 4ª casa decimal, tornando a aproximação bem precisa.

Séries de Maclaurin

Ainda na matemática, as séries de Maclaurin são um caso particular da Série de Taylor, considerando a centralização da aproximação em torno de c = 0.

Se substituirmos na Série de Taylor o valor de c= 0, obtemos a seguinte série:

Vamos expandir essa série para três funções que apresentam derivadas bem conhecidas: senx, cosx e e^x.

Expansão de sen(x) e cos(x)

Tomando-se a função sen(x), temos as seguintes derivadas:

f'(x) = cos(x)

f’’(x) = - sen(x)

f’’’(x) = -cos(x)

f⁽⁴⁾(x) = sen(x)

f⁽⁵⁾(x) = cos(x)

Não precisa ser nenhum gênio da Matemática, dominando cálculo integral e diferencial, para perceber que, a partir da 4ª derivada, tudo se repete. Além disso, a primeira derivada já é a função cosx e tudo igualmente se repete.

Como precisamos dos valores em torno de 0 (zero), agora ficou bem fácil determinar os termos, sabendo-se apenas que sen(0) = 0 e cos(0) = 1.

Sendo assim, temos as belíssimas expressões para a aproximação das funções senx e cosx:

Se você se formou em Engenharia, em algum momento, você ouviu seu professor de cálculo dizendo que “para valores pequenos de x, sen(x) = x e cos(x) = 1”.

Vamos fazer esse teste para sen(x): suponha que x = 0,1.

Então a expressão do sen(x) fica:

Calculando essa expressão, você chegará ao valor 0,099833416667, que é aproximadamente 0,1. Isso porque 0,1 é pequeno. Elevado ao cubo e dividido por 3!, fica menor ainda. Elevado à 5ª potência e dividido por 5! (120), vira quase zero!

Expansão da função exponencial e^x

Já vimos aqui no Engenharia 360 uma matéria explicando as particularidades do número “e”.

Uma delas é que, se usado como base de uma função exponencial, f(x) = e^x, as suas derivadas são a própria função! Isso é ótimo, porque as n derivadas serão e^x e, consequentemente, avaliada em c = 0, sabemos que qualquer número elevado a 0 resulta 1.

Portanto, para a função exponencial, temos a bela aproximação:

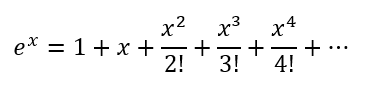
Por fim, se considerarmos nessa expressão x = 1? Aí teremos uma série para obtenção do número “e”, resultando na soma infinita apresentada abaixo:

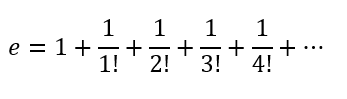
Gostou de aprender sobre as Séries de Taylor e Maclaurin? Agora, aplique esse conhecimento em seus estudos e pesquisas!

Fonte: Wikipedia e Wikipedia 2.

Imagens: Todos os Créditos reservados aos respectivos proprietários (sem direitos autorais pretendidos). Caso eventualmente você se considere titular de direitos sobre algumas das imagens em questão, por favor entre em contato com contato@engenharia360.com para que possa ser atribuído o respectivo crédito ou providenciada a sua remoção, conforme o caso.

Cristiano Oliveira da Silva

Engenheiro Civil; formado pela Escola Politécnica da Universidade de São Paulo; com conhecimentos em 'BIM Manager at OEC'; promove palestras com foco em Capacitação e Disseminação de BIM / Soft Skills.