Você já ouviu falar nas equações de Navier-Stokes? Elas são um conjunto de fórmulas que buscam prever o comportamento dos fluidos (líquidos e gases), suas propriedades e seu movimento. Pense em uma nuvem se formando, um rio correndo, o sangue circulando, um navio flutuando ou um avião voando. Essas equações buscam justamente descrever as propriedades dos fluidos, sua pressão, velocidade e trajetória em cada ponto.
A história por trás da elaboração das equações de Navier-Stokes
As equações de Navier-Stokes foram desenvolvidas no século XIX por Claude-Louis Navier e George Stokes, se baseando fortemente nos trabalhos de seus antecessores, como a família Bernoulli. Apesar de desenvolvidas, até hoje essas equações não apresentam uma solução exata e única, e você pode ficar milionário se conseguir resolvê-las.
O desafio de resolver estas difíceis equações
Estas equações fazem parte do Millenium Prize, uma série de prêmios fornecido pelo Clay Mathematics Institute, que fornecerá 1 milhão de dólares para quem conseguir uma solução analítica, única e suave dessas equações. E, afinal, por que elas são tão difíceis de serem resolvidas? Isso deve-se porque são equações diferenciais parciais que, além de envolver inúmeras incógnitas, são altamente não-lineares e vetoriais (pois devem ser solucionadas nas 3 dimensões, além do tempo). Dê uma olhada em um caso geral dessas equações abaixo:
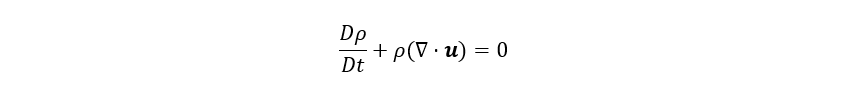
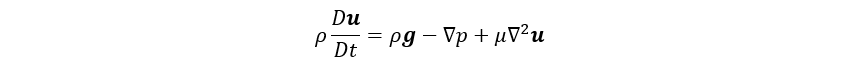
Equação 1
É denominada Equação da Conservação da Massa (conhecida também como Equação da Continuidade) e ela, como o nome indica, se baseia no fato de que a massa não é criada ou destruída em um dado ponto de um sistema, apenas rearranjada.
Equação 2
É denominada Equação da Quantidade de Movimento, é basicamente a aplicação da segunda lei de Newton (que dita que a força resultante em um dado sistema é dado pelo produto de sua massa por sua aceleração) para um sistema fluido, extrapolado para todas as dimensões. Mais abaixo teremos essas equações escritas de uma forma mais "simples", bem como a definição de cada símbolo.
As aplicações das equações de Navier-Stokes
Os avanços tecnológicos que a solução dessas equações traria são inúmeras e, além da exatidão na previsão do comportamento dos fluidos, um dos principais desmembramentos dessa solução é a análise da turbulência, sendo um evento aleatório e caótico. As ferramentas matemáticas que deverão ser empregadas para a solução das equações de Navier-Stokes poderão ser empregadas, posteriormente, para a análise de eventos aleatórios, probabilidade, inteligência artificial, gerando uma exatidão muito maior nesses comportamentos e, assim, ampliando muito a sua aplicação.
PUBLICIDADE
CONTINUE LENDO ABAIXO
LEIA MAIS
Então, se essas equações ainda não foram resolvidas, como temos tantos avanços nessa área? Como conseguimos prever hoje o comportamento dos fluidos e analisar seus comportamentos? Como conseguimos saber se o avião vai voar ou não? A realidade é que, apesar de não haver solução exata, as equações de Navier-Stokes são amplamente utilizadas nas mais diversas áreas.
Simulações de aerodinâmica
O que ocorre é que, para cada aplicação diferente (por exemplo: uma análise aerodinâmica da asa de um avião difere da análise meteorológica para sabermos se vai chover amanhã) nós fazemos algumas suposições sobre o comportamento e simplificamos essas equações. Em conjunto com técnicas matemáticas de simulação discreta, como o Método dos Elementos Finitos, essas soluções podem ser aproximadas e as equações de Navier-Stokes podem ser resolvidas.
Você talvez já tenha visto a foto da “aerodinâmica da vaca” (abaixo), e isso nada mais é do que a solução das Equações de Navier-Stokes, com alguma simplificação, do vento ao redor de uma vaca. Esse diagrama colorido indica, justamente, alguma das características do fluido (velocidade, no caso) em cada ponto do domínio (já adiantamos que a simulação da vaca apresenta algumas inconsistências, para os curiosos).
PUBLICIDADE
CONTINUE LENDO ABAIXO
Buscando entrar brevemente na parte mais técnica das equações para os mais curiosos, as equações de Navier-Stokes, de forma expandida (entenda: com menos termos matemáticos complexos), é descrito abaixo:
Equação da Continuidade:
Equação da Quantidade de Movimento em cada direção (x, y e z) separadamente:
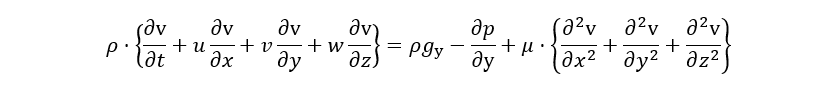
Abaixo, segue uma breve descrição do significado de cada termo:
Conclusão
Enfim, as equações de Navier-Stokes são um dos maiores desafios matemáticos da atualidade, mas mesmo sem uma solução exata os engenheiros utilizam os mais diversos artifícios para conseguir trabalhar com elas. Estou na torcida para que você, leitor, consiga resolver estas equações (e se lembre de nós depois do prêmio).
E aí, gostou do conteúdo? Não esqueça de comentar abaixo!
Veja Também: Decolagem histórica do maior avião movido a hidrogênio em fotos
Imagens: Todos os Créditos reservados aos respectivos proprietários (sem direitos autorais pretendidos). Caso eventualmente você se considere titular de direitos sobre algumas das imagens em questão, por favor entre em contato com contato@engenharia360.com para que possa ser atribuído o respectivo crédito ou providenciada a sua remoção, conforme o caso.
Comentários
Victor Peron
Engenheiro Mecânico formado pela Fundação Educacional Inaciana (FEI); especialista em Administração Industrial; com mestrado com ênfase em Energia de Fluidos pela Escola Politécnica da USP; formação extracurricular em Matemática Aplicada no curso da Prandiano; e também experiência em CFD, utilizando principalmente o método dos elementos espectrais em solvers de código aberto.
